Introduction to Algorithms:

Computational Complexity

by Vasyl Nakvasiuk, 2013

What is an algorithm?

What is an Algorithm?


An algorithm is a procedure that takes any of the possible input instances and transforms it to the desired output.


Important issues: correctness, elegance and efficiency.

Efficiency

Is this really necessary?

Criteria of efficiency:

  • Time complexity
  • Space complexity



Time complexity ≠ Space complexity ≠ Complexity of algorithm

How can we measure complexity?

How can we measure complexity?


Empirical Analysis (Benchmarks)

Theoretical Analysis (Asymptotic analysis)

Benchmarks

Empirical Analysis

Benchmarks

Version #1


What means “fast”?

Benchmarks

Version #2


import time

start = time.time() # Return the time in seconds since the epoch.
my_algo(some_input)
end = time.time()

print(end - start)
					

0.048032498359680176

Benchmarks

Version #3


import timeit

timeit.timeit('my_algo(some_input)', number=1000)
					

1000 loops, best of 3: 50.3 ms per loop

Benchmarks

Version #4


import timeit

inputs = [1000, 10000, 500000, 1000000]

for input in inputs:
    timeit.timeit('my_algo(input)', number=1000)
					

list of 1000 items:
1000 loops, best of 3: 50.3 ms per loop

list of 10000 items:
1000 loops, best of 3: 104.7 ms per loop

list of 500000 items:
1000 loops, best of 3: 459.1 ms per loop

list of 1000000 items:
1000 loops, best of 3: 3.12 s per loop

Benchmarks

Version #5


# Intel Core i7-3970X @ 3.50GHz, RAM 8 Gb, Ubuntu 12.10 x64, Python 3.3.0

import timeit

inputs = [1000, 10000, 500000, 1000000]

for input in inputs:
    timeit.timeit('my_algo(input)', number=1000)
					

list of 1000 items:
1000 loops, best of 3: 50.3 ms per loop

list of 10000 items:
1000 loops, best of 3: 104.7 ms per loop

list of 500000 items:
1000 loops, best of 3: 459.1 ms per loop

list of 1000000 items:
1000 loops, best of 3: 3.12 s per loop

Experimental studies have several limitations:


  • It is necessary to implement and test the algorithm in order to determine its running time.
  • Experiments can be done only on a limited set of inputs, and may not be indicative of the running time on other inputs not included in the experiment.
  • In order to compare two algorithms, the same hardware and software environments should be used.

Asymptotic analysis

Theoretical Analysis

Asymptotic analysis

Efficiency as a function of input size


T(n) – running time as a function of n, where n – size of input.

n → ∞

Random-Access Machine (RAM)

Best, worst, and average-case complexity


Linear search


def linear_search(my_item, items):
    for position, item in enumerate(items):
        if my_item == item:
            return position

T(n) = n ?

T(n) = 1/2 ⋅ n ?

T(n) = 1 ?

Best, worst, and average-case complexity


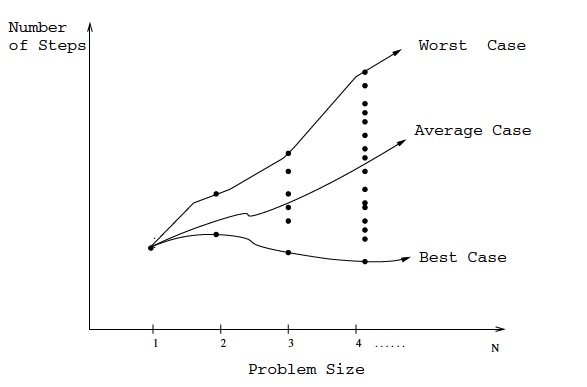
Best, worst, and average-case complexity


Linear search


def linear_search(my_item, items):
    for position, item in enumerate(items):
        if my_item == item:
            return position

Worst case: T(n) = n

Average case: T(n) = 1/2 ⋅ n

Best case: T(n) = 1


T(n) = O(n)

How can we compare two functions?


We can use Asymptotic notation

Asymptotic notation

The Big Oh Notation

Asymptotic upper bound


O(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ c⋅g(n) for all n ≥ n0}


T(n) ∈ O(g(n))

or

T(n) = O(g(n))

Ω-Notation

Asymptotic lower bound


Ω(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ c⋅g(n) ≤ f(n) for all n ≥ n0}


T(n) ∈ Ω(g(n))

or

T(n) = Ω(g(n))

Θ-Notation

Asymptotic tight bound


Θ(g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1⋅g(n) ≤ f(n) ≤ c2⋅g(n) for all n ≥ n0}


T(n) ∈ Θ(g(n))

or

T(n) = Θ(g(n))

Graphic examples of the Θ, O and Ω notations


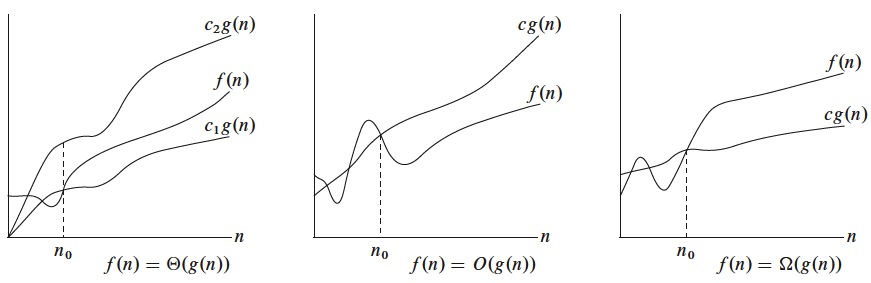
Examples


3⋅n2 - 100⋅n + 6 = O(n2),
because we can choose c = 3 and
3⋅n2 > 3⋅n2 - 100⋅n + 6


100⋅n2 - 70⋅n - 1 = O(n2),
because we can choose c = 100 and
100⋅n2 > 100⋅n2 - 70⋅n - 1


3⋅n2 - 100⋅n + 6 ≈ 100⋅n2 - 70⋅n - 1

Linear search


Linear search (Villarriba version):

T(n) = O(n)


Linear search (Villabajo version)


def linear_search(my_item, items):
    for position, item in enumerate(items):
        print('position – {0}, item – {0}'.format(position, item))
        print('Compare two items.')
        if my_item == item:
            print('Yeah!!!')
            print('The end!')
            return position

T(n) = O(3⋅n + 2) = O(n)

Speed of "Villarriba version" ≈ Speed of "Villabajo version"

Types of Order


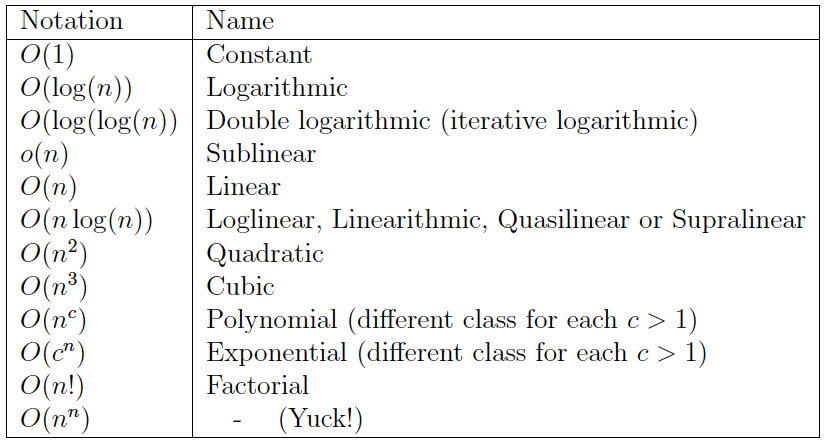
However, all you really need to understand is that:

n! ≫ 2n ≫ n3 ≫ n2 ≫ n⋅log(n) ≫ n ≫ log(n) ≫ 1

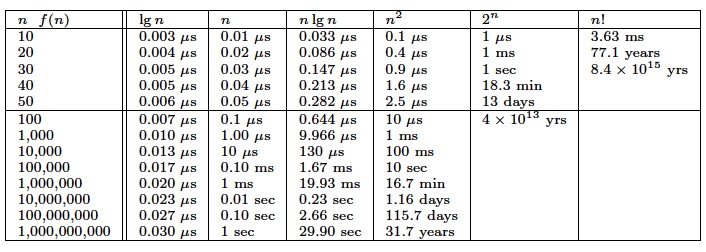
The Big Oh complexity for different functions


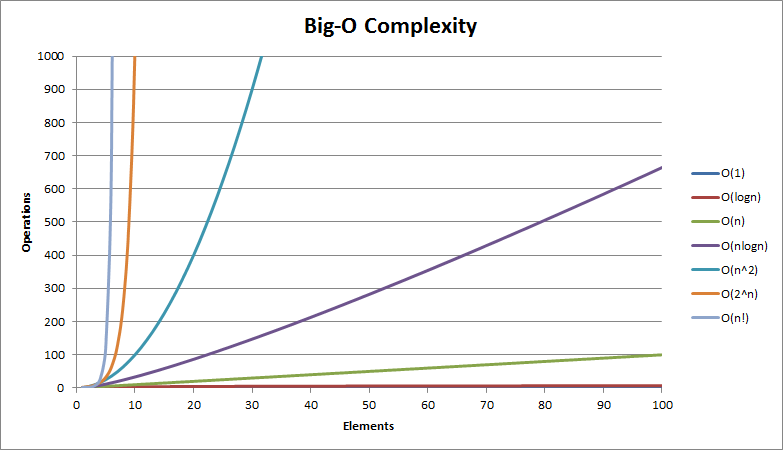
Growth rates of common functions measured in nanoseconds

Each operation takes one nanosecond (10-9 seconds).

CPU ≈ 1 GHz


Binary search



def binary_search(seq, t):
    min = 0; max = len(seq) - 1
    while 1:
        if max < min:
            return -1
        m = (min + max) / 2
        if seq[m] < t:
            min = m + 1
        elif seq[m] > t:
            max = m - 1
        else:
            return m

T(n) = O(log(n))

Practical usage

Add DB “index”

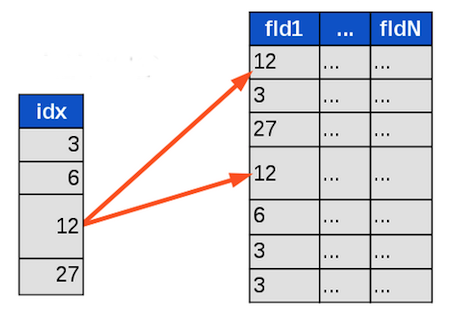
Search with index vs Search without index

Binary search vs Linear search

O(log(n)) vs O(n)

How can you quickly find out complexity?

O(?)

On the basis of the issues discussed here, I propose that members of SIGACT, and editors of computer science and mathematics journals, adopt the O, Ω and Θ notations as defined above, unless a better alternative can be found reasonably soon.

D. E. Knuth, "Big Omicron and Big Omega and BIg Theta", SIGACT News, 1976.

Benchmarks
or
Asymptotic analysis?


Use both approaches!

Summary

  1. We want to predict running time of an algorithm.
  2. Summarize all possible inputs with a single “size” parameter n.
  3. Many problems with “empirical” approach (measure lots of test cases with various n and then extrapolate).
  4. Prefer “analytical” approach.
  5. To select best algorithm, compare their T(n) functions.
  6. To simplify this comparision “round” the function using asymptotic (“big-O”) notation
  7. Amazing fact: Even though asymptotic complexity analysis makes many simplifying assumptions, it is remarkably useful in practice: if A is O(n3) and B is O(n2) then B really will be faster than A, no matter how they’re implemented.

Links


Books:

  • “Introduction To Algorithms, Third Edition”, 2009, by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein
  • “The Algorithm Design Manual, Second Edition”, 2008, by Steven S. Skiena


Other:

The end


Thank you for attention!

  • Vasyl Nakvasiuk
  • Email: vaxxxa@gmail.com
  • Twitter: @vaxXxa
  • Github: vaxXxa


This presentation:

Source: https://github.com/vaxXxa/talks

Live: http://vaxXxa.github.io/talks